SW Studying

상관분석(Correlation Analysis)이란?

- 두 연속 변수가 서로 관련이 있는지 검정하는 통계 분석 기법 (H0: 두 변수 간 관계 없다 / H1: 관계 있다)

상관계수(Correlation Coefficient)란?

- 상관분석을 통해 도출되고 상관계수를 통해 두 변수가 얼마나 관련되어 있는지, 관련성의 정도 파악 가능

- 상관계수는 0~1 사이의 값을 지니고 1에 가까울수록 관련성이 크다는 것을 의미

   → 상관계수가 양수: 정비례 관계

   → 상관계수가 음수: 반비례 관계

■ ggplot2 패키지의 economics 데이터를 이용해서 실업자 수와 개인 소비 지출의 상관관계 분석

- R에 내장된 cor.test()를 이용하여 상관분석 

economics <- as.data.frame(ggplot2::economics)
cor.test(economics$unemploy, economics$pce)

① 실업자 수와 개인 소비 지출의 상관이 통계적으로 유의하다

    - 출력 결과의 p-value를 계산하면 0.05 미만인 것을 알 수 있다.

② 'cor'

    - 'cor'은 상관계수를 의미. 상관계수가 양수 0.61이므로, 실업자 수와 개인 소비 지출은 한 변수가 증가하면 다른 변수가 증가하는 정비례 관계임을 알 수 있다.

■ 상관행렬 히트맵 만들기

- 여러 변수의 관련성을 한 번에 보고자 할 경우, 모든 변수의 상관 관계를 나타낸 상관행렬(Correlation Matrix)를 만들고, 상관행렬을 보면 어떤 변수끼리 관련이 크고 적은지 파악할 수 있음.

1. cor()을 이용하여 상관행렬 만들기

- R에 내장된 mtcars 데이터를 이용할 예정 (mtcars는 자동차 32종의 11개 속성에 대한 정보를 담고 있는 데이터)

car_cor <- cor(mtcars)  #상관행렬 생성
round(car_cor, 2)       #소수점 셋째 자리에서 반올림해 출력

① 연비 별 실린더 수

    - mpg(연비) 행과 cyl(실린더 수) 열이 교차되는 부분을 보면 상관계수가 -0.85임을 볼 수 있다. 상관계수가 음수면 반비례한다는 의미이므로 연비가 높을수록 실린더 수가 적은 경향이 있다는 것을 알 수 있다.

② 실린더 수 별 무게

    - cyl(실린더 수)과 wt(무게)의 상관계수가 0.78이므로 정비례한다. 따라서 실린더 수가 많을수록 자동차가 무거운 경향이 있다는 것을 알 수 있다.

2. 상관행렬을 히트맵으로 만들기

- 여러 변수로 상관행렬을 만들면 변수들의 관계를 파악하기 쉽지 않음

- 상관행렬을 히트맵(heat map)으로 만들면 변수들의 관계 쉽게 파악 가능 (corrplot 패키지의 corrplot()을 이용)

cf) 히트맵(heat map): 값의 크기를 색깔로 표현한 그래프

install.packages("corrplot")
library(corrplot)

corrplot(car_cor)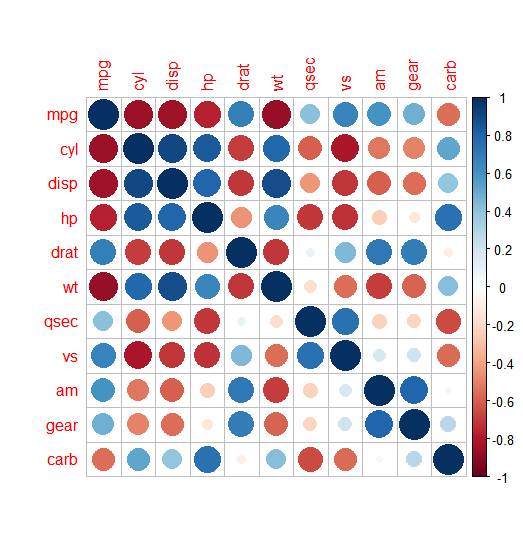

>> 상관계수가 클수록 원의 크기가 크고 색깔이 진하고, 상관계수가 양수면 파란색, 음수면 빨간색 계열로 표현되어 있음. 원의 크기와 색깔을 보면 상관관계 정도와 방향 쉽게 파악 가능

3. 그래프 형태 바꾸기

- corrplot()의 파라미터를 이용해 그래프 형태를 다양하게 바꾸는 것이 가능. method에 "number"를 지정하여 원 대신 상관계수가 표현되도록 설정 가능

corrplot(car_cor, method = "number")

4. 다양한 파라미터 지정

- 그래프 색깔을 바꾸기 위해 colorRampPalette()로 색상 코드 목록을 생성한 후 col 파라미터에 지정

col <- colorRampPalette(c("#BB4444", "#EE9988", "#FFFFFF", "#77AADD", "#4477AA"))
corrplot(car_cor,
         method = "color",        # 색깔로 표현
         col = col(200),          # 색상 200개 선정
         type = "lower",          # 왼쪽 아래 행렬만 표시
         order = "hclust",        # 유사한 상관계수끼리 군집화
         addCoef.col = "black",   # 상관계수 색깔
         tl.col = "black",        # 변수명 색깔
         tl.srt = 45,             # 변수명 45도 기울임
         diag = F)                # 대각 행렬 제외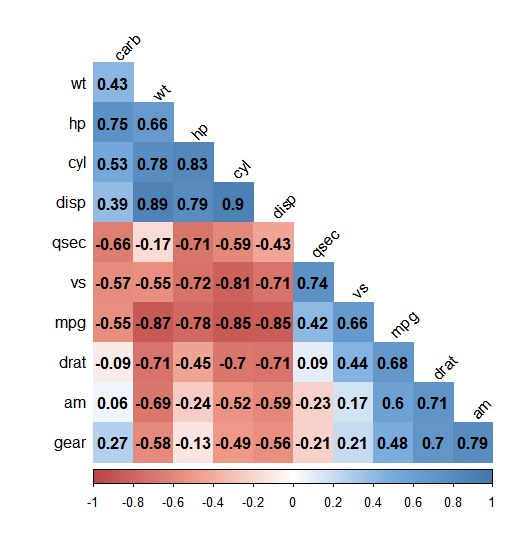

(참고자료: Visualize correlation matrix using correlogram: http://www.sthda.com/english/wiki/visualize-correlation-matrix-using-correlogram

(출처; 가천대학교 컴퓨터공학과, 이영호 교수님)

(출처; 쉽게 배우는 R 데이터 분석, 김영우)

작년 MBC스페셜 '10년 후의 세계 - 멋진 신세계와 일자리 도둑'에서 4차산업혁명으로 빠르게 변해 가고 있는 우리 사회의 모습을 다뤘다. 

MBC 홈페이지에서는 '로봇이 당신의 일자리를 빼앗을까요?'라는 질문에 자신의 직업을 입력하면 10년 후 그 직업이 로봇으로 대체될 가능성을 보여준다. 

관심 있는 사람은 하단 링크를 통해 들어갈 수 있다.

http://event.imbc.com/2025myjob/

t 검정(t-test)란?

- 두 집단의 평균에 통계적으로 유의한 차이가 있는지 알아볼 때 사용하는 통계 분석 기법

- R에 내장된 t.test()를 이용해 t 검정 가능

■ ggplot2 패키지의 mpg 데이터를 이용해 compact 자동차와 suv 자동차의 도시 연비 t 검정을 수행

(1) mpg 데이터를 불러와 class, cty 변수만 남긴 뒤 class 변수가 "compact"인 자동차와 "suv"인 자동차를 추출

mpg <- as.data.frame(ggplot2::mpg)
library(dplyr)
mpg_diff <- mpg %>%
  select(class, cty) %>%
  filter(class %in% c("compact","suv"))
head(mpg_diff)

table(mpg_diff$class)

(2) t.test()를 이용해 t 검정

- 추출한 mpg_diff 데이터를 지정하고, ~ 기호를 이용해 비교할 값인 cty(도시 연비) 변수와 비교할 집단인 class(자동차 종류) 변수 지정

- t 검정은 비교하는 집단의 분산이 같은지 여부에 따라 적용하는 공식이 다름. (여기서는 집단 간 분산이 같다고 가정하고 var.equal 에 T를 지정)

t.test(data = mpg_diff, cty ~ class, var.equal = T)

① 출력된 t 검정 결과에서 'p-value'가 유의확률을 의미

(블로그 좌측 [Probability $ Statistics >> Lecture Summary] 의 '통계적 가설 검정이란?' 포스팅 참고)

    - 일반적으로 유의확률 5%를 판단 기준으로 삼고, p-value가 0.05 미만이면 '집단 간 차이가 통계적으로 유의하다'고 해석. 실제로는 차이가 없는데 이런 정도의 차이가 우연히 관찰된 확률이 5%보다 작다면, 이 차이를 우연이라고 보기 어렵다는 결론. 'p-value < 2.2e - 16'은 유의확률이 2.2*10^-16 보다 작다는 의미이므로 여기서 p-value가 0.05보다 작다는 의미이다.

따라서 이 분석 결과는 'compact 와 suv 간 평균 도시 연비 차이가 통계적으로 유의하다'고 해석할 수 있다.

② 'sample estimates'

    - 'sample estimates' 부분을 보면 각 집단의 cty 평균이 나타나 있음. "compact"는 20인 반면, "suv"는 13이므로, "suv"보다 "compact"의 도시 연비가 더 높다고 할 수 있음

(출처; 가천대학교 컴퓨터공학과, 이영호 교수님)

(출처; 쉽게 배우는 R 데이터 분석, 김영우)

■ 기술 통계와 추론 통계

- 기술 통계(Descriptive statistics): 데이터를 요약해 설명하는 통계 기법 (ex. 사람들이 받는 월급을 집계해 전체 월급 평균을 구함 / EDA 과정을 거쳐 데이터를 설명)

- 추론 통계(Inferential statistics): 단순히 숫자를 요약하는 것을 넘어 어떤 값이 발생할 확률을 계산하는 통계 기법

(ex. 수집된 데이터에서 성별에 따라 월급에 차이가 있는 것으로 나타났을 때, 이런 차이가 우연히 발생할 확률을 계산해서 이 확률이 0.05 작다면 성별에 따른 월급 차이가 통계적으로 유의하다(statistically significant)고 결론 내린다. 반대로 이런 차이가 우연히 나타날 확률이 0.05보다 크다면 성별에 따른 월급 차이가 통계적으로 유의하지 않다(not statistically significant)고 결론 내린다.

통계적으로 유의하다(statistically significant) = p-value가 0.05보다 작다

통계적으로 유의하지 않다(not statistically significant) = p-value가 0.05보다 크거나 같다.

(p-value = 오류. 왜 0.05인지는 밑에서 설명)

■ 통계적 가설 검정

통계적 가설 검정(Statistical hypothesis test)란?

- 유의확률을 이용해 가설을 검정하는 방법

유의확률(Significance probability, p-value)란?

- 실제로는 집단 간 차이가 없는데 우연히 차이가 있는 데이터가 추출될 확률을 의미

1. 가설의 종류

** 귀무가설(영가설): 0이다, 존재하지 않는다. (H0)

** 대립가설(위와 대립되는 가설): 0이 아니다, 존재 한다. (H1)

2. 가설검정(Hypothesis test)

- 객관적인 증거는 일반적으로 95% 정도 필요 == 오류가 5% 이하

① 객관적인 증거 95%↓  =  오류 5% ↑   ☞  H0

② 객관적인 증거 95%↑  =  오류 5% ↓   ☞  H1

3. 유의수준 ( 제 1종 오류 (α) )

- 제 1종 오류 (α): H0이 참인데, H1으로 잘못 선택하는 오류  >>  오류를 기준으로 잡음. 5% 이하의 오류

(출처; 가천대학교 컴퓨터공학과, 이영호 교수님)